Recursive queries are a type of database query that involves recursively traversing and querying hierarchical or self-referential data structures. They are particularly useful for querying data that has a nested or hierarchical representation. Recursive queries enable developers to navigate and process these complex data structures by iteratively applying a set of rules or conditions until a termination criterion is met.

Recursive queries in SQL

Recursive queries were introduced as part of the SQL:1999 standard which is known as SQL3, a major revision to the SQL language1. Prior to SQL3, SQL lacked built-in support for querying hierarchical or recursive data structures like organizational charts, bill-of-materials data, and network/graph data. The introduction of recursive queries in SQL3 empowered developers to effectively query hierarchical or self-referential data structures. Unlike traditional SQL queries that operate on a static set of rows, recursive queries enable traversal and manipulation of hierarchical data structures by iteratively executing an anchor and recursive member.

SQL uses common table expression (CTE) which is a temporary result buffer to create the recursive queries. It is supported by popular database management (PostgreSQL, SQL server, Oracle, MySQL V8)2. Pandiani has a nice post showing the power of recursive queries using MySQL in diverse scenarios, such as sequence generation, fibonacci calculation and, hierarchical data traversal3.

The key components of a recursive SQL query are:

  • Anchor member: Serving as the base case, the anchor member initializes the recursive query by fetching the initial set of rows.
  • Recursive member: Acting as the inductive step, the recursive member retrieves additional rows by joining with the results from the previous iteration of the query. A termination condition is necessary to stop the recursion.
  • WITH clause: This defines the recursive common table expression (CTE) by combining the anchor and recursive members using UNION or UNION ALL.

Example of recursive queries in SQL

Let’s see an example to understand recursive queries better. Say we have a users table containing names and cities, and a friendships table defining relationships between users:

alt Friendships Figure: Friendship network among users

MySQL (used version 8.0.36) commands to defines the tables and populate them with the data:

-- Create the users table
CREATE TABLE users (
  name VARCHAR(50) PRIMARY KEY,
  city VARCHAR(50)
);

-- Insert sample data into the users table
INSERT INTO users (name, city) VALUES
('Alex', 'Chicago'),
('Bob', 'Detroit'),
('Carter', 'Chicago'),
('David', 'Atlanta'),
('Ethan', 'Boston');

-- Create the friendships table
CREATE TABLE friendships (
  user_name VARCHAR(50),
  friend_name VARCHAR(50),
  FOREIGN KEY (user_name) REFERENCES users(name) ON DELETE CASCADE,
  FOREIGN KEY (friend_name) REFERENCES users(name) ON DELETE CASCADE
);

-- Insert sample data into the friendships table
INSERT INTO friendships (user_name, friend_name) VALUES
('Alex', 'Bob'), 
('Alex', 'Carter'),
('Bob', 'David'),
('Carter', 'David'),
('David', 'Ethan');


SELECT * FROM users;
+--------+---------+
| name   | city    |
+--------+---------+
| Alex   | Chicago |
| Bob    | Detroit |
| Carter | Chicago |
| David  | Atlanta |
| Ethan  | Boston  |
+--------+---------+
5 rows in set (0.01 sec)

SELECT * FROM friendships;
+-----------+-------------+
| user_name | friend_name |
+-----------+-------------+
| Alex      | Bob         |
| Alex      | Carter      |
| Bob       | David       |
| Carter    | David       |
| David     | Ethan       |
+-----------+-------------+
5 rows in set (0.00 sec)

Recursive query to find connection to a specific city using SQL

To find all users connected to Chicago through friend connections, we can use a recursive query:

-- Recursive query to find users from Chicago or connected to Chicago through friends
WITH RECURSIVE FriendsGraph AS (
  -- Base case: Select users directly associated with Chicago
  SELECT name, city
  FROM users
  WHERE city = 'Chicago'
  
  UNION ALL
  
  -- Recursive case: Find friends of users in the previous iteration
  SELECT f.friend_name, u.city
  FROM FriendsGraph fg
  JOIN friendships f ON f.user_name = fg.name
  JOIN users u ON f.friend_name = u.name
  WHERE u.city != 'Chicago'  -- Terminate recursion if friend is not from Chicago
)
-- Query to select all users connected to Chicago through friends
SELECT DISTINCT name, city
FROM FriendsGraph;

+--------+---------+
| name   | city    |
+--------+---------+
| Alex   | Chicago |
| Carter | Chicago |
| Bob    | Detroit |
| David  | Atlanta |
| Ethan  | Boston  |
+--------+---------+
5 rows in set (0.00 sec)

The anchor member retrieves all users directly from Chicago. The recursive member joins the previous results with the friendships table to find more friends iteratively. The city != 'Chicago' condition terminates recursion when all friends from Chicago have been found.

Recursive query to compute transitive closure using SQL

Transitive closure represents the complete set of relationships derived from a given set of initial relationships by following all possible paths. Here’s an example of how we could compute the transitive closure of friendships using a recursive query:

WITH RECURSIVE TransitiveClosure AS (
  SELECT user_name, friend_name
  FROM friendships
  UNION
  SELECT tc.user_name, f.friend_name
  FROM TransitiveClosure tc
  JOIN friendships f ON tc.friend_name = f.user_name
)
SELECT * FROM TransitiveClosure;

+-----------+-------------+
| user_name | friend_name |
+-----------+-------------+
| Alex      | Bob         |
| Alex      | Carter      |
| Bob       | David       |
| Carter    | David       |
| David     | Ethan       |
| Alex      | David       |
| Bob       | Ethan       |
| Carter    | Ethan       |
| Alex      | Ethan       |
+-----------+-------------+
9 rows in set (0.00 sec)

The anchor member enlists the direct friendships. The recursive member joins the previous results to find friends of friends, recursing until no new friendships are discovered.

Recursive query in Datalog

Datalog is a declarative logic programming language that is specialized to execute recursive queries efficiently. It is based on the logic programming paradigm and allows users to express recursive relationships and rules in a concise and declarative manner. Datalog programs consist of facts and rules. Facts represent the base data, while rules define the logical relationships and inferences that can be derived from the facts. Recursive rules enable the expression of recursive relationships, making Datalog a natural fit for handling recursive queries.

Let’s implement the above recursive queries in Datalog. First, we need to define the users and friendships relations and add facts to these relations:

.decl users(name: symbol, city: symbol)
.decl friendships(user_name: symbol, friend_name: symbol)

// Facts
users("Alex", "Chicago").
users("Bob", "Detroit").
users("Carter", "Chicago").
users("David", "Atlanta").
users("Ethan", "Boston").

friendships("Alex", "Bob").
friendships("Alex", "Carter").
friendships("Bob", "David").
friendships("Carter", "David").
friendships("David", "Ethan").

Recursive query to find connection to a specific city using Datalog

In Datalog, we need to define a base rule which sets the initial results and a recursive rule that recursively derive the new facts from existing facts based on the initial result set. In the following Datalog program, we recursively derive the users who are connected to Chicago by themselves or through friends.

.decl connectedToChicago(name: symbol, city: symbol)
// Base rule
connectedToChicago(X, Y) :- users(X, "Chicago"), users(X, Y).
// Recursive rule
connectedToChicago(Z, U) :- connectedToChicago(X, Y), friendships(X, Z), users(Z, U), U != "Chicago".
.output connectedToChicago

In this program, the base rule initializes the result set by selecting users who reside in Chicago directly. It sets the initial facts that serve as the starting point for the recursive derivation of additional facts. The recursive rule iteratively derives new facts by traversing the friendships network to find users indirectly connected to Chicago through friends. In the recursive rule, the connectedToChicago(X, Y) condition matches existing facts in the connectedToChicago relation, which represents users already known to be connected to Chicago. The friendships(X, Z) condition checks if the user X from the previous step has a friend Z in the friendships relation. The users(Z, U) condition retrieves the city U of the friend Z from the users relation. U != "Chicago" condition ensures that the recusion stops when the friend Z is from Chicago avoiding infinite loops by revisiting Chicago residents. If all the conditions are satisfied, the rule creates a new fact connectedToChicago(Z, U) in the connectedToChicago relation, effectively adding the friend Z and their city U to the result set.

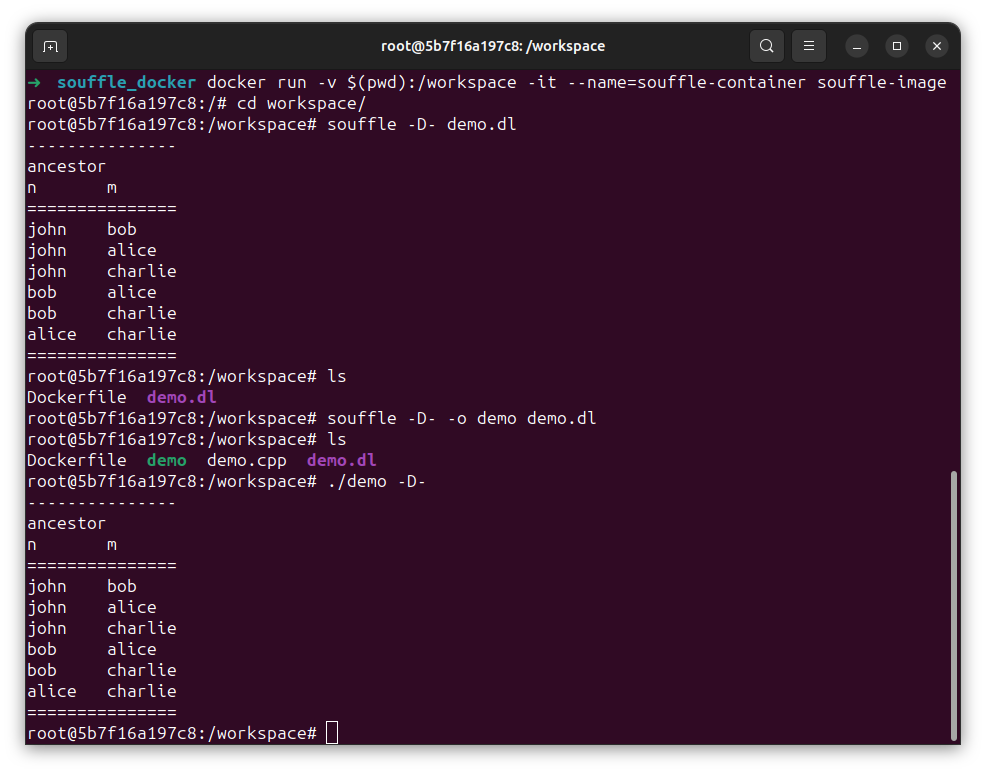
Running the program using Soufflé (Soufflé installation guide can be found in Install Soufflé on Ubuntu using Docker), we get the following users who are connected to Chicago:

connectedToChicago
name	city
===============
Alex	Chicago
Bob  Detroit
Carter	Chicago
David	Atlanta
Ethan	Boston

Recursive query to compute transitive closure using Datalog

The last example is to compute transitive closure of friendships. It can be implemented concisely in Datalog with two simple rules:

// Declare the TC relation
.decl tc(user_name: symbol, connected_user_name: symbol)
// Base rule
tc(X, Y) :- friendships(X, Y).
// Recursive rule
tc(X, Z) :- friendships(X, Y), tc(Y, Z).
.output tc

The base rule states that if there’s a direct friendship between X and Y in the friendships relation, then X is connected to Y (represented by tc(X, Y)). This captures the initial set of connections. The recursive rule states that if there’s a friendship between X and Y (from friendships), and Y is already connected to another user Z (based on a previous recursive call or the base rule), then X is also indirectly connected to Z (represented by tc(X, Z)). This allows the program to explore connections beyond direct friendships, iteratively building the transitive closure.

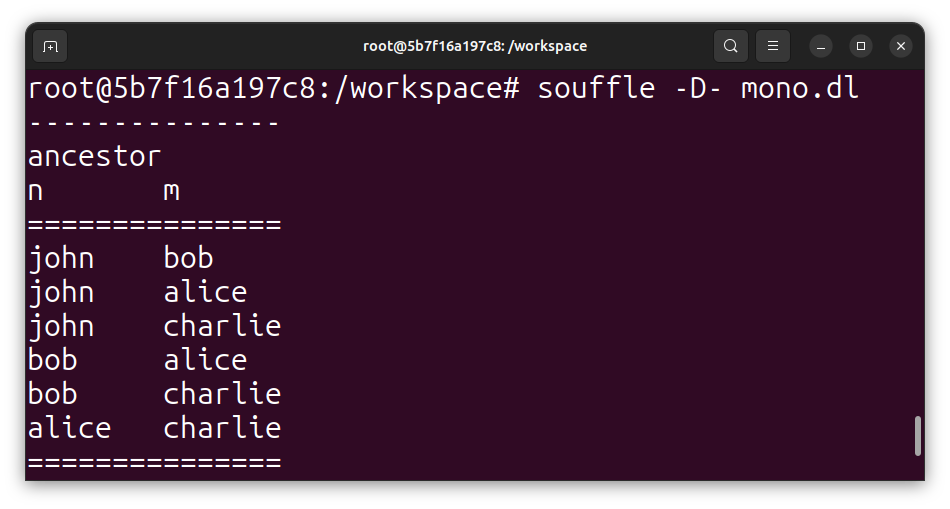
If we run the program with Soufflé (Soufflé installation guide can be found in Install Soufflé on Ubuntu using Docker), we can infer the following facts as transitive closure graph of the friendships relation:

souffle -D- tc.dl
---------------
tc
n	    m
===============
Alex	Bob
Alex	Carter
Alex	David
Alex	Ethan
Bob	    David
Bob	    Ethan
Carter  David
Carter  Ethan
David	Ethan
===============

Advantages of Datalog over SQL for recursive queries

While SQL provides built-in support for recursive queries, Datalog, as a declarative logic programming language, is more naturally suited for expressing and executing recursive queries.

Few key points why Datalog is better than SQL for handling recursive queries:

  • Simplicity: Datalog programs are more concise and easier to read and write than their SQL counterparts, especially for complex recursive queries. The declarative nature of Datalog focuses on specifying the logic rather than the procedural details of how to evaluate the recursion.
  • Expressiveness: Datalog has a richer set of language constructs for expressing recursive relationships and constraints, making it more expressive than SQL for certain types of recursive queries, such as those involving transitive closure or least fixed-point computations.
  • Flexibility: SQL systems typically impose a maximum recursion depth. For instance, the default recursion depth limit in MySQL is 1000 (set by the cte_max_recursion_depth4 variable)5. While this depth can be adjusted, it remains a constraint. In contrast, Datalog engines operate without a hard limit on maximum recursion depth, offering greater flexibility and scalability.
  • Execution time constraint: In MySQL, another limitation often encountered is the max_execution_time setting, which restricts the duration a query can run. Once this threshold is reached, the query is terminated, potentially interrupting recursive operations. Conversely, Datalog engines typically offer more leniency in terms of execution time constraints, allowing recursive queries to run without being abruptly terminated.
  • Optimization: Datalog engines, like Soufflé, are specifically designed to optimize and evaluate recursive queries efficiently. They employ techniques like magic set transformations, query rewriting, and incremental view maintenance, which can outperform the recursive query evaluation strategies used in traditional database systems.
  • Integration with other declarative paradigms: Datalog can be seamlessly integrated with other declarative paradigms, such as constraint handling rules (CHR) or answer set programming (ASP), enabling the development of more expressive and powerful knowledge representation systems.
  • Reasoning capabilities: Datalog’s foundations in logic programming make it well-suited for reasoning tasks, such as deductive databases, policy analysis, and program analysis, which often involve recursive queries.

While SQL is a powerful and widely adopted language for working with relational data, Datalog offers advantages for handling recursive queries, particularly in scenarios where conciseness, expressiveness, and efficient evaluation of recursion are crucial.

References

  1. Recursive query evaluation and Datalog By Sudeepa Roy [return]
  2. Recursive SQL Queries: Exploring Hierarchical Data Management [return]
  3. Introduction to MySQL 8.0 Recursive Common Table Expression (Part 2) by Corrado Pandiani [return]
  4. MySQL documentation on cte_max_recursion_depth [return]
  5. MySQL blog on recursive CTE by Guilhem Bichot [return]

Advertisement

Citation

Click to select citation style

Shovon, A. R. (2024, April 23). Recursive queries in SQL and Datalog. Ahmedur Rahman Shovon. Retrieved June 22, 2024, from https://arshovon.com/blog/recursive-queries/

Shovon, Ahmedur Rahman. “Recursive queries in SQL and Datalog.” Ahmedur Rahman Shovon, 23 Apr. 2024. Web. 22 Jun. 2024. https://arshovon.com/blog/recursive-queries/.

@misc{ shovon_2024,
    author = "Shovon, Ahmedur Rahman",
    title = "Recursive queries in SQL and Datalog",
    year = "2024",
    url = "https://arshovon.com/blog/recursive-queries/",
    note = "[Online; accessed 22-June-2024]"
}
Related contents in this website
Introduction to Datalog as logic programming
Introduction to Datalog as logic programming
declarative programming
Monotonic and nonmonotonic reasoning in Datalog
Monotonic and nonmonotonic reasoning in Datalog
declarative programming
Install Soufflé on Ubuntu using Docker
Install Soufflé on Ubuntu using Docker
declarative programming
Recursive queries in SQL and Datalog
Previous post

Monotonic and nonmonotonic reasoning in Datalog

Recursive queries in SQL and Datalog
Next post

Introduction to Datalog as logic programming

Ahmedur Rahman Shovon
Ahmedur Rahman Shovon
PhD Student (Computer Science) at University of Illinois Chicago