Divide and conquer strategy and merge sort

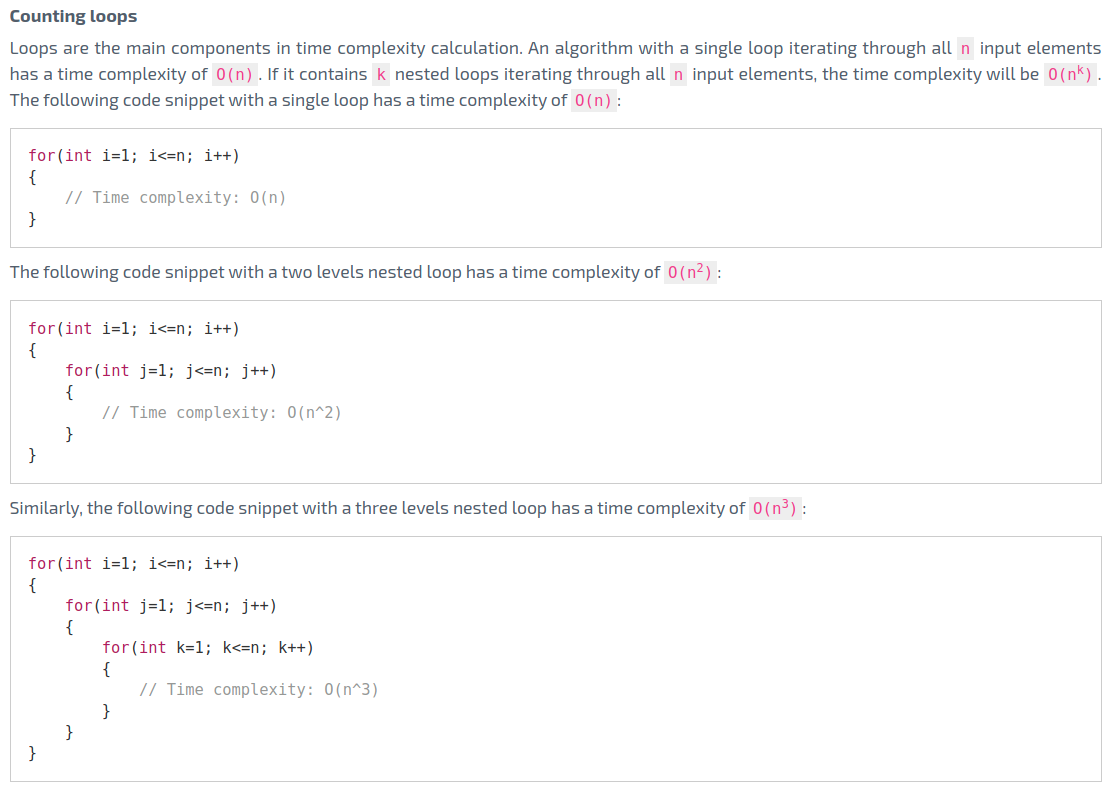
In a divide and conquer strategy, a problem is divided into multiple subproblems. These subproblems are similar to the original problem but smaller in size. The divide and conquer strategy solves these subproblems recursively. Then it combines the solutions of the subproblems to develop a final solution for the original problem. Thus, the divide and conquer strategy has two parts: divide and conquer.

Divide

In the divide phase, the original problem is divided into smaller subproblems. Each subproblem has the same characteristics as the original problem.

Conquer

In this phase, the subproblems are solved recursively. Finally, the smaller results are combined to form the final solution of the original problem.

Merge sort is based on the divide and conquer strategy. To sort an array of n elements, it follows the below steps:

  • It divides the unsorted array into n/2 parts recursively until there is only one element in each part.
  • It sorts the smaller parts and combines the smaller solutions to create the final result.

The following figure illustrates how merge sort follows the divide and conquer strategy.

Merge sort splitting and merging step

Merge sort characteristics

Practical

Merge sort is an efficient comparison-based sorting algorithm. As of Perl 5.8, merge sort is the default sorting algorithm. The Linux kernel also uses merge sort for linked lists.

Not Adaptive

Merge sort is not adaptive. It performs the same on sorted, almost sorted, and unsorted lists. Its performance is not dependent on whether the input data is sorted or not.

Offline

Merge sort works after receiving all the data. It does not sort the element when it receives them.

Stable

Merge sort is stable. Numbers with the same value appear in the output array as they appear in the input array. Let's take an input array A = [3, 0, 3]. In the input array, the value 3 occurs two times; at index 0 and 2. Insertion sort ensures that in the output array, the occurrences of 3 are placed in the same order as the input array.

Not In place:

Merge sort does not sort the input list in place. It requires an additional list of n size to sort unsorted list of n elements. So, its space complexity is O(n).

Loglinear time complexity

It has loglinear time complexity.

  • Worst Time complexity (Big-O): O(nlogn), where n: total number of elements in the list.
  • Average Time complexity (Big-Theta): Θ(nlogn), where n: total number of elements in the list.
  • Best Time complexity (Big-Omega): Ω(nlogn), where n: total number of elements in the list.
  • Space complexity: O(n)

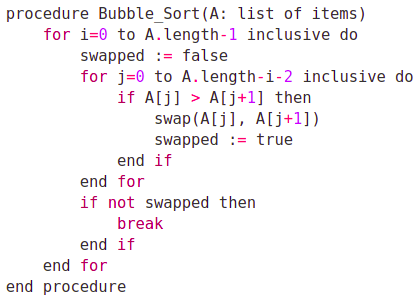
Merge Sort algorithm pseudocode

procedure Merge(A: list of items, TEMP: temporary array, LEFT, MID, RIGHT)
    LEFT_POS := 0
    RIGHT_POS := MID + 1
    CURRENT_POS := LEFT
    while LEFT_POS <= MID and RIGHT_POS <= RIGHT do
        if A[LEFT_POS] <= A[RIGHT_POS] then
            TEMP[CURRENT_POS] := A[LEFT_POS]
            LEFT_POS := LEFT_POS + 1
        else then
            TEMP[CURRENT_POS] := A[RIGHT_POS]
            RIGHT_POS := RIGHT_POS + 1
        end if
        CURRENT_POS := CURRENT_POS + 1
    end while
    while LEFT_POS <= MID do
        TEMP[CURRENT_POS] := A[LEFT_POS]
        LEFT_POS := LEFT_POS + 1
        CURRENT_POS := CURRENT_POS + 1
    end while
    while RIGHT_POS <= RIGHT do
        TEMP[CURRENT_POS] := A[RIGHT_POS]
        RIGHT_POS := RIGHT_POS + 1
        CURRENT_POS := CURRENT_POS + 1
    end while
    for i in LEFT to RIGHT inclusive do
        A[i] = TEMP[i]
    end for
end procedure

procedure Split_And_Merge(A: list of items, TEMP: temporary array, LEFT, RIGHT)
    if LEFT < RIGHT then
        MID := ⌊(LEFT + RIGHT)⌋ / 2
        Split_And_Merge(A, TEMP, LEFT, MID)
        Split_And_Merge(A, TEMP, MID+1, RIGHT)
        Merge(A, TEMP, LEFT, MID, RIGHT)
    end if
end procedure

procedure Merge_Sort(A: list of items, N: total items)
    TEMP[0..A.LENGTH] a new array
    Split_And_Merge(A, TEMP, 0, N - 1)
end procedure

Merge Sort implementation using Python 3

"""
Implementation of merge sort algorithm

Main File: merge_sort.py
Test File: test_merge_sort.py
"""


def get_merge_sorted_numbers(numbers):
    """ Returns sorted list for a given list

    Arguments:
    numbers -- list of numbers
    """
    temp = numbers.copy()
    perform_split_and_merge(numbers, temp, 0, len(numbers) - 1)
    return numbers


def perform_split_and_merge(ar, temp, left, right):
    if left < right:
        mid = (right + left) // 2
        perform_split_and_merge(ar, temp, left, mid)
        perform_split_and_merge(ar, temp, mid + 1, right)
        perform_merge(ar, temp, left, mid, right)


def perform_merge(ar, temp, left, mid, right):
    left_pos = left
    right_pos = mid + 1
    current_pos = left
    while left_pos <= mid and right_pos <= right:
        if ar[left_pos] <= ar[right_pos]:
            temp[current_pos] = ar[left_pos]
            left_pos += 1
        else:
            temp[current_pos] = ar[right_pos]
            right_pos += 1
        current_pos += 1
    while left_pos <= mid:
        temp[current_pos] = ar[left_pos]
        left_pos += 1
        current_pos += 1
    while right_pos <= right:
        temp[current_pos] = ar[right_pos]
        right_pos += 1
        current_pos += 1
    for i in range(left, right + 1):
        ar[i] = temp[i]

Unit testing merge sort implementation using Python 3

"""
Unittest of merge sort implementation

Main File: merge_sort.py
Test File: test_merge_sort.py
"""
import unittest
from merge_sort import get_merge_sorted_numbers


class TestMergeSort(unittest.TestCase):
    def test_get_merge_sorted_numbers_positive_unsorted(self):
        test_case = [2, 3, 1, 4, 2, 4]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_positive_negative_unsorted(self):
        test_case = [2, -3, 1, -4, 2, 4]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_same_values_positive(self):
        test_case = [1, 1, 1, 1]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_same_values_negative(self):
        test_case = [-1, -1, -1]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_single_item(self):
        test_case = [1]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_empty_list(self):
        test_case = []
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_positive_reverse(self):
        test_case = [123, 56, 8]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_positive_negative_reverse(self):
        test_case = [1, 0, -1]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_negative_reverse(self):
        test_case = [-1, -3, -56]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")

    def test_get_merge_sorted_numbers_positive_negative_floating(self):
        test_case = [-1.5, 3.336, -66.3, 5]
        expected_result = sorted(test_case)
        test_result = get_merge_sorted_numbers(test_case.copy())
        self.assertEqual(expected_result, test_result,
                         f"Failed on {test_case}, "
                         f"Expected {expected_result}, "
                         f"Found {test_result}")


if __name__ == "__main__":
    unittest.main()
Unittest run
Figure: Unittest of merge sort implementation

Merge Sort implementation using C++

#include <bits/stdc++.h>

using namespace std;


void perform_merge(int ar[], int temp[], int left, int mid, int right)
{
    int left_pos = left;
    int right_pos = mid + 1;
    int current_pos = left;
    while (left_pos <= mid && right_pos <= right)
    {
        if (ar[left_pos] <= ar[right_pos])
        {
            temp[current_pos++] = ar[left_pos++];
        }
        else
        {
            temp[current_pos++] = ar[right_pos++];
        }
    }
    while (left_pos <= mid)
    {
        temp[current_pos++] = ar[left_pos++];
    }
    while (right_pos <= right)
    {
        temp[current_pos++] = ar[right_pos++];
    }
    for(int i=left; i <= right; i++)
    {
        ar[i] = temp[i];
    }
}


void perform_split_and_merge(int ar[], int temp[], int left, int right)
{
    if(left < right)
    {
        int mid = (left + right) / 2;
        perform_split_and_merge(ar, temp, left, mid);
        perform_split_and_merge(ar, temp, mid+1, right);
        perform_merge(ar, temp, left, mid, right);
    }
}

void get_merge_sorted_numbers(int ar[], int n)
{
    int temp[n];
    perform_split_and_merge(ar, temp, 0, n-1);
}

void print_array(int ar[], int n)
{
    for(int i=0; i<n; i++)
    {
        cout << ar[i] << " ";
    }
    cout << "" <<endl;
}

int main()
{
    int n = 6;
    int ar[] = {2, -3, 1, -4, 2, 4};
    cout << "Before sorting: ";
    print_array(ar, n);
    get_merge_sorted_numbers(ar, n);
    cout << "After sorting: ";
    print_array(ar, n);
    return 0;
}

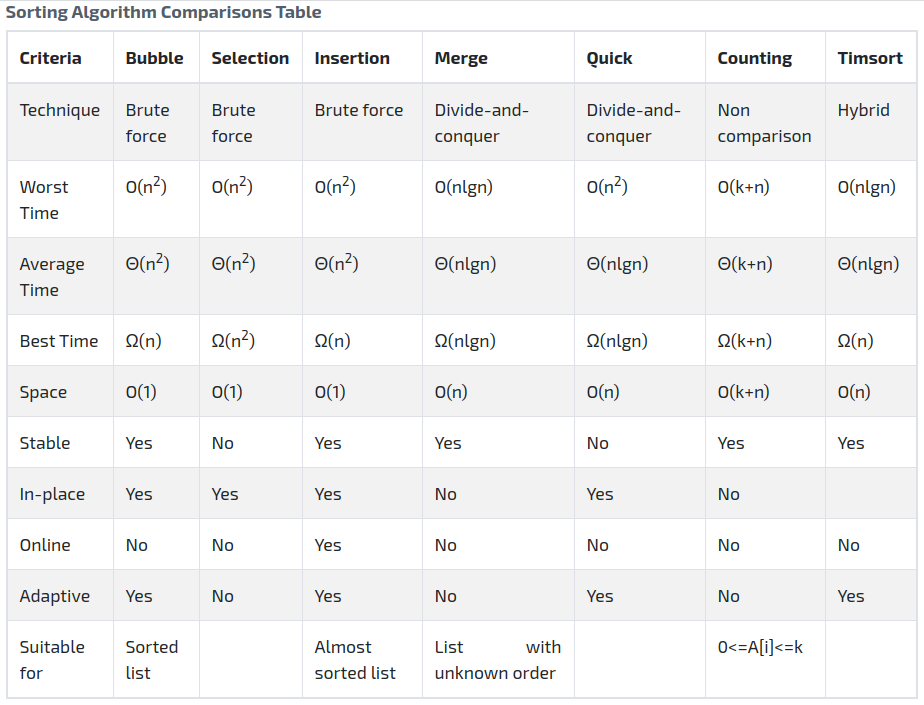
Comparison between bubble sort and insertion sort

  • Insertion sort is more efficient than bubble sort as it requires fewer swaps to sort the elements.
  • Insertion sort is online, but bubble sort is offline. That means insertion sort sorts the elements when receiving each element but bubble sort sorts the elements only after receiving all the elements.

The following table shows the execution time in seconds for merge sort, bubble sort, and insertion sort for different numbers of input elements.

Set SizeMaximum ValueMerge sortBubble sortInsertion sortCounting sort
100010000.02285 seconds0.51674 seconds0.24463 seconds0.00209 seconds
200020000.04808 seconds2.14491 seconds0.97831 seconds0.00433 seconds
300030000.07648 seconds5.05203 seconds2.2953 seconds0.00654 seconds
400040000.10607 seconds9.82914 seconds4.19266 seconds0.0091 seconds
500050000.14967 seconds15.07934 seconds6.75124 seconds0.01975 seconds
600060000.31401 seconds21.08818 seconds9.4236 seconds0.01431 seconds
700070000.20681 seconds29.10378 seconds13.71728 seconds0.01677 seconds
800080000.24075 seconds39.52925 seconds17.08021 seconds0.0192 seconds
900090000.25785 seconds48.37365 seconds21.51451 seconds0.0225 seconds
10000100000.30643 seconds59.90875 seconds25.93183 seconds0.02465 seconds

This result is generated using timeit module of Python with the following code.

"""
Compare execution time between merge sort, bubble sort, insertion sort, and counting sort
"""
from timeit import timeit
import random
import json

data = {
    "input_sizes": [],
    "max_values": [],
    "data": {
        "labels": [],
        "datasets": [{
            "label": 'Merge sort',
            "data": [],
            "fill": False,
            "borderColor": 'red',
            "backgroundColor": 'red',
            "tension": 0.1
        }, {
            "label": 'Bubble sort',
            "data": [],
            "fill": False,
            "borderColor": 'green',
            "backgroundColor": 'green',
            "tension": 0.1
        }, {
            "label": 'Insertion sort',
            "data": [],
            "fill": False,
            "borderColor": 'blue',
            "backgroundColor": 'blue',
            "tension": 0.1
        }, {
            "label": 'Counting sort',
            "data": [],
            "fill": False,
            "borderColor": 'yellow',
            "backgroundColor": 'yellow',
            "tension": 0.1
        }]
    }
}


"""
Implementation of merge sort algorithm

Main File: merge_sort.py
Test File: test_merge_sort.py
"""


def get_merge_sorted_numbers(numbers):
    """ Returns sorted list for a given list

    Arguments:
    numbers -- list of numbers
    """
    temp = numbers.copy()
    perform_split_and_merge(numbers, temp, 0, len(numbers) - 1)
    return numbers


def perform_split_and_merge(ar, temp, left, right):
    if left < right:
        mid = (right + left) // 2
        perform_split_and_merge(ar, temp, left, mid)
        perform_split_and_merge(ar, temp, mid + 1, right)
        perform_merge(ar, temp, left, mid, right)


def perform_merge(ar, temp, left, mid, right):
    left_pos = left
    right_pos = mid + 1
    current_pos = left
    while left_pos <= mid and right_pos <= right:
        if ar[left_pos] <= ar[right_pos]:
            temp[current_pos] = ar[left_pos]
            left_pos += 1
        else:
            temp[current_pos] = ar[right_pos]
            right_pos += 1
        current_pos += 1
    while left_pos <= mid:
        temp[current_pos] = ar[left_pos]
        left_pos += 1
        current_pos += 1
    while right_pos <= right:
        temp[current_pos] = ar[right_pos]
        right_pos += 1
        current_pos += 1
    for i in range(left, right + 1):
        ar[i] = temp[i]



def get_bubble_sorted_numbers(numbers):
    """ Returns a sorted list of numbers using bubble sort

    Arguments:
    numbers -- list of numbers
    """
    for i in range(len(numbers)):
        swapped = False
        for j in range(len(numbers) - i - 1):
            if numbers[j] > numbers[j + 1]:
                numbers[j], numbers[j + 1] = numbers[j + 1], numbers[j]
                swapped = True
        if not swapped:
            break
    return numbers


def get_insertion_sorted_numbers(numbers):
    """ Returns a sorted list of numbers using insertion sort

    Arguments:
    numbers -- list of numbers
    """
    for i in range(1, len(numbers)):
        value = numbers[i]
        j = i - 1
        while j >= 0 and numbers[j] > value:
            numbers[j + 1] = numbers[j]
            j -= 1
        numbers[j + 1] = value
    return numbers


def get_counting_sorted_numbers(numbers, max_value):
    """ Returns a sorted list of non negative using counting sort

    Arguments:
    numbers -- list of non negative integers within max_value
    max_value -- non negative integer
    """
    sorted_numbers = [None] * len(numbers)
    counts = [0] * (max_value + 1)
    for i in numbers:
        counts[i] += 1
    counts[0] -= 1
    for i in range(1, max_value + 1):
        counts[i] += counts[i - 1]
    for i in numbers[::-1]:
        sorted_numbers[counts[i]] = i
        counts[i] -= 1
    return sorted_numbers


def update_execution_time():
    global data
    merge_execution_time = round(
        timeit('result=get_merge_sorted_numbers(unsorted.copy())',
               globals=globals(), number=MAX_ITERATION), 5)
    bubble_execution_time = round(
        timeit('result=get_bubble_sorted_numbers(unsorted.copy())',
               globals=globals(), number=MAX_ITERATION), 5)
    insertion_execution_time = round(
        timeit('result=get_insertion_sorted_numbers(unsorted.copy())',
               globals=globals(), number=MAX_ITERATION), 5)
    counting_execution_time = round(timeit(
        'result=get_counting_sorted_numbers(unsorted.copy(), MAX_NUMBER)',
        globals=globals(), number=MAX_ITERATION), 5)
    execution_times = [merge_execution_time, bubble_execution_time,
                       insertion_execution_time, counting_execution_time]
    for i in range(len(data["data"]["datasets"])):
        current_execution_time = {
            "x": MAX_NUMBER,
            "y": execution_times[i]
        }
        data["data"]["datasets"][i]["data"].append(current_execution_time)
    data["data"]["labels"].append(str(MAX_NUMBER))
    data["input_sizes"].append(MAX_NUMBER)
    data["max_values"].append(MAX_NUMBER)


def print_output(data):
    print("| Set Size | Maximum Value | ", end="")
    for algorithm in data["data"]["datasets"]:
        print(algorithm["label"] + " | ", end="")
    print("")
    for i in range(len(data["data"]["datasets"]) + 2):
        if i == 0:
            print("| ", end="")
        print("--- | ", end="")
    print("")
    for i in range(len(data["input_sizes"])):
        print(f'| {data["input_sizes"][i]} | {data["max_values"][i]} | ',
              end="")
        for j in range(len(data["data"]["datasets"])):
            print(f'{data["data"]["datasets"][j]["data"][i]["y"]} seconds | ',
                end="")
        print("")
    print(json.dumps(data["data"], indent=2))


if __name__ == "__main__":
    MAX_ITERATION = 10
    for i in range(1000, 10001, 1000):
        MAX_NUMBER = i
        unsorted = [random.randint(0, MAX_NUMBER) for i in range(MAX_NUMBER)]
        update_execution_time()
    print_output(data)

Practice challenges

Easy difficulty challenges:

Hard difficulty challenges:

Reference

Advertisement

Cite This Work
APA Style
Shovon, A. R. (2021, April 29). Merge Sort. Ahmedur Rahman Shovon. Retrieved March 29, 2024, from https://arshovon.com/blog/merge-sort/
MLA Style
Shovon, Ahmedur Rahman. “Merge Sort.” Ahmedur Rahman Shovon, 29 Apr. 2021. Web. 29 Mar. 2024. https://arshovon.com/blog/merge-sort/.
BibTeX entry
@misc{ shovon_2021,
    author = "Shovon, Ahmedur Rahman",
    title = "Merge Sort",
    year = "2021",
    url = "https://arshovon.com/blog/merge-sort/",
    note = "[Online; accessed 29-March-2024; URL: https://arshovon.com/blog/merge-sort/]"
}
Related Contents in this Website
Bubble Sort
algorithm
Understanding Time Complexity
algorithm
Sorting Algorithm Comparisons
algorithm
Previous Post

Bubble Sort

Next Post

Sorting a list (Python 3)

Ahmedur Rahman Shovon
Ahmedur Rahman Shovon
PhD Student (Computer Science) at University of Illinois Chicago