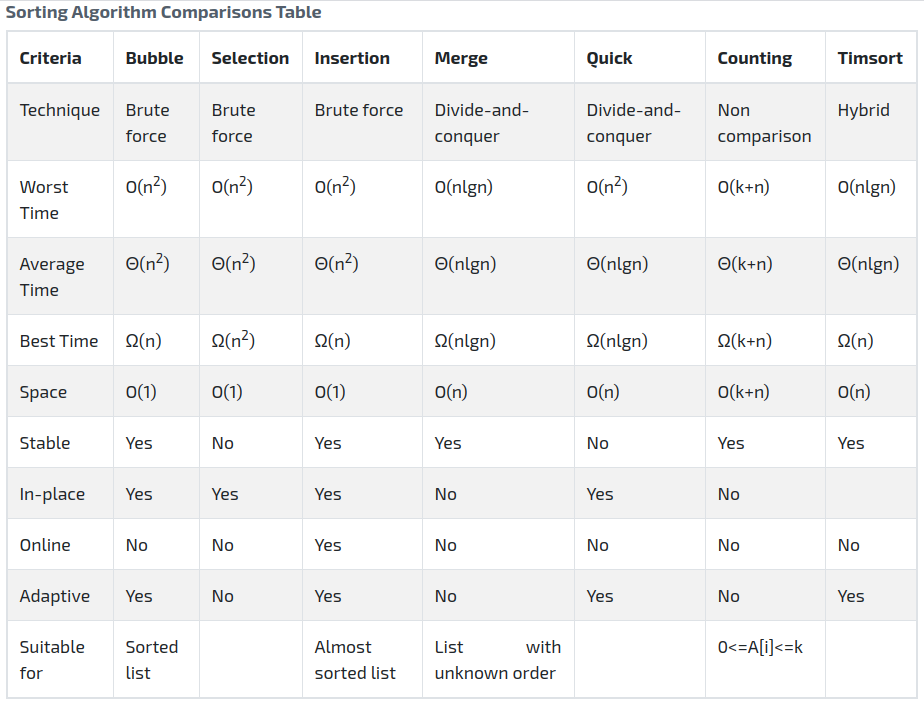
Characteristics
Simple implementation
Insertion sort can be implemented easily with less lines of code. It is quite efficient for small data sets. Though it has same complexity than other quadratic sorting algorithms like selection sort or bubble sort, insertion sort is more efficient.
Adaptive
Insertion sort is adaptive. If the input data set is already sorted, the number of steps are reduced.
Online
Insertion sort works on the data as it receives it. The dataset is always sorted in each step of the insertion sort. A practical example of insertion sort is sorting a hand of playing cards. Assume, at the beginning of a card game, we have no cards in the left hand. Then we take a face down card from the table and search for it's position in the left hand. To find the correct position for a card we compare the newly drawn card with each of the cards in the left hand from left to right. Then when we find the suitable spot, we insert the card into it's correct position. At any times, the cards in the left hand are sorted.
Stable
Insertion sort is stable. Numbers with the same value appears in the output array as they appear in the input array. Let's take an input array A = [3, 0, 3]. In the input array the value 3 occurs 2 times; at index 0 and 2. Insertion sort ensures that in the output array the occurrences of 3 are placed as same order as of the input array.
In place:
Insertion sort sorts the input list in place. It does not require additional list to sort the elements. It only requires a constant amount of additional memory space O(1).
Quadratic time complexity
It has a quadratic time complexity.
- Worst Time complexity (Big-O):
O(n*n), wheren: total number of elements in the list. - Average Time complexity (Big-Theta):
Θ(n*n), wheren: total number of elements in the list. - Best Time complexity (Big-Omega):
Ω(n), wheren: total number of elements in the list. - Space complexity:
O(1)
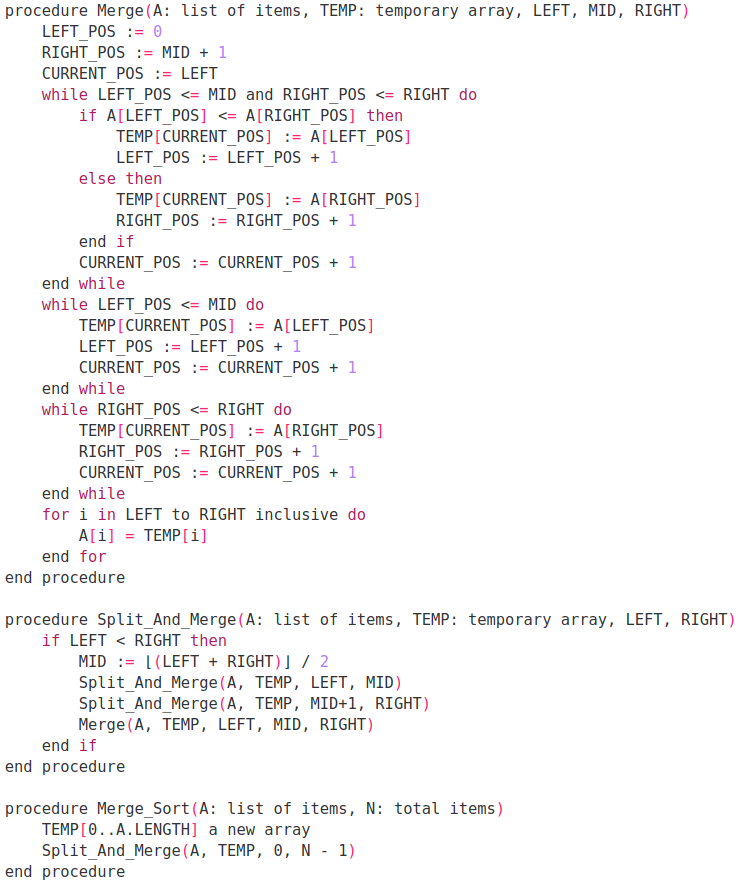
Algorithm Pseudocode
Insertion_Sort(A)
for i=1 to A.length-1
value = A[i]
j = i - 1
while j >= 0 and A[j] > value
A[j+1] = A[j]
j = j - 1
A[j+1] = value
Implementation using Python 3
"""
Implementation of insertion sort algorithm
Main File: insertion_sort.py
Test File: test_insertion_sort.py
"""
def get_insertion_sorted_numbers(numbers):
""" Returns sorted list for a given list
Arguments:
numbers -- list of numbers
"""
for i in range(1, len(numbers)):
j = i - 1
value = numbers[i]
while j >= 0 and numbers[j] > value:
numbers[j + 1] = numbers[j]
j -= 1
numbers[j + 1] = value
return numbers
Unit testing insertion sort implementation using Python 3
"""
Unittest of insertion sort implementation
Main File: insertion_sort.py
Test File: test_insertion_sort.py
"""
import unittest
from insertion_sort import get_insertion_sorted_numbers
class TestInsertionSort(unittest.TestCase):
def test_get_bubble_sorted_numbers_positive_unsorted(self):
test_case = [2, 3, 1, 4, 2, 4]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_positive_negative_unsorted(self):
test_case = [2, -3, 1, -4, 2, 4]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_same_values_positive(self):
test_case = [1, 1, 1, 1]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_same_values_negative(self):
test_case = [-1, -1, -1]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_single_item(self):
test_case = [1]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_empty_list(self):
test_case = []
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_positive_negative_reverse(self):
test_case = [1, 0, -1]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_negative_reverse(self):
test_case = [-1, -3, -56]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
def test_get_bubble_sorted_numbers_positive_negative_floating(self):
test_case = [-1.5, 3.336, -66.3, 5]
expected_result = sorted(test_case)
test_result = get_insertion_sorted_numbers(test_case.copy())
self.assertEqual(expected_result, test_result,
f"Failed on {test_case}, "
f"Expected {expected_result}, "
f"Found {test_result}")
if __name__ == "__main__":
unittest.main()
Difference between Insertion Sort and Counting Sort
- Insertion sort is a quadratic sorting algorithm where as counting sort uses linear time to sort a set of unsorted integers.
- Insertion sort's worst case performance is
O(n*n)where as counting sort's worst case performance isO(k+n)[Insertion sort - Wiki][Counting sort - Wiki]. - Though insertion sort has worse time complexity than the counting sort, it is more memory efficient. It requires only
O(1)constant space where as counting sort requiresO(k+n)space. - Another import difference between this two sorting algorithms is the online characteristics. Insertion sort works on live feeding data but counting sort works only after gathering full dataset.
The following table shows the comparison between insertion sort and counting sort based on the execution time.
| Set Size | Maximum Value | Insertion Sort Time | Counting Sort Time |
|---|---|---|---|
| 10 | 10 | 0.03347 seconds | 0.02473 seconds |
| 1000 | 1000 | 2.59963 seconds | 0.02278 seconds |
| 10000 | 10000 | 29.85276 seconds | 0.02672 seconds |
This result is generated using timeit module of Python with the following code.
"""
Compare execution time between insertion sort and counting sort
"""
from timeit import timeit
import random
def get_insertion_sorted_numbers(numbers):
""" Returns sorted list for a given list
Arguments:
numbers -- list of numbers
"""
for i in range(1, len(numbers)):
j = i - 1
value = numbers[i]
while j >= 0 and numbers[j] > value:
numbers[j + 1] = numbers[j]
j -= 1
numbers[j + 1] = value
return numbers
def get_counting_sorted_numbers(numbers, max_value):
""" Returns a sorted list of non negative using counting sort
Arguments:
numbers -- list of non negative integers within max_value
max_value -- non negative integer
"""
sorted_numbers = [None] * len(numbers)
counts = [0] * (max_value + 1)
for i in numbers:
counts[i] += 1
counts[0] -= 1
for i in range(1, max_value + 1):
counts[i] += counts[i - 1]
for i in numbers[::-1]:
sorted_numbers[counts[i]] = i
counts[i] -= 1
return sorted_numbers
if __name__ == "__main__":
MAX_NUMBER = 10
small_list = [random.randint(0, MAX_NUMBER) for i in range(MAX_NUMBER)]
insertion_execution_time = timeit(
'result=get_insertion_sorted_numbers(small_list.copy())',
globals=globals(), number=10000)
counting_execution_time = timeit(
'result=get_counting_sorted_numbers(small_list.copy(), MAX_NUMBER)',
globals=globals(), number=10000)
print(f"Data set of {MAX_NUMBER} numbers:")
print(f"Insertion sort took: {insertion_execution_time:.5f} seconds")
print(f"Counting sort took: {counting_execution_time:.5f} seconds")
MAX_NUMBER = 1000
medium_list = [random.randint(0, MAX_NUMBER) for i in range(MAX_NUMBER)]
insertion_execution_time = timeit(
'result=get_insertion_sorted_numbers(medium_list.copy())',
globals=globals(), number=100)
counting_execution_time = timeit(
'result=get_counting_sorted_numbers(medium_list.copy(), MAX_NUMBER)',
globals=globals(), number=100)
print(f"Data set of {MAX_NUMBER} numbers:")
print(f"Insertion sort took: {insertion_execution_time:.5f} seconds")
print(f"Counting sort took: {counting_execution_time:.5f} seconds")
MAX_NUMBER = 10000
large_list = [random.randint(0, MAX_NUMBER) for i in range(MAX_NUMBER)]
insertion_execution_time = timeit(
'result=get_insertion_sorted_numbers(large_list.copy())',
globals=globals(), number=10)
counting_execution_time = timeit(
'result=get_counting_sorted_numbers(large_list.copy(), MAX_NUMBER)',
globals=globals(), number=10)
print(f"Data set of {MAX_NUMBER} numbers:")
print(f"Insertion sort took: {insertion_execution_time:.5f} seconds")
print(f"Counting sort took: {counting_execution_time:.5f} seconds")
Practice challenges
Easy difficulty challenges:
Reference
- Introduction to algorithms by Cormen, Thomas H and Leiserson, Charles E and Rivest, Ronald L and Stein, Clifford
- Insertion sort Wikipedia article
- timeit module documentation
- Counting sort
- Bubble sort
- Sorting Algorithm Comparisons
Advertisement