Introduction to Datalog as logic programming

Declarative programming

Declarative programming is focused on specifying the desired result of a computation, without explicitly defining the step-by-step procedures (also known as control flow) to achieve that result¹. It focuses on answering the question of what to achieve, rather than how to achieve it. This contrasts with imperative programming (e.g. C++, Python, JavaScript, Java etc.), which is focused on specifying the exact sequence of instructions (the how) to perform a specific task or reach a desired result (the what).

A prime example of a declarative language is SQL (Structured Query Language) widely used for managing and querying relational databases². In SQL, queries describe the desired result of a computation (the what), without specifying the exact steps to compute that result (the how). For example, consider the following simple SQL query:

SELECT * FROM users WHERE users.city='Chicago';

This query instructs the database system to return all the records from the users relation where the city is Chicago. The query does not indicate how the database should execute this operation. Instead, the query interpreter of the database system is responsible for creating an optimal execution plan to generate the desired result.

Datalog as Logic programming

Logic programming is a subset of declarative programming. In logic programming, the programmer specifies a set of logical facts and rules about a domain and the logic programming system uses logical inference to derive the desired results. Prolog and Datalog are two popular logic programming languages. As the title suggests, this tutorial will focus on Datalog mostly. Logic programming has three key features¹:

• No side effect: Programs do not modify state outside their scope.
• No explicit control flow: The order of execution is determined by logical inference, not by explicit control structures like loops or conditionals.
• Strong guarantees about termination: Datalog programs are guaranteed to terminate for all inputs (Prolog does not guarantee that), avoiding infinite loops or non-termination issues.

📝 Datalog, a logic programming language, extends relational algebra and supports recursion as core feature.

Stratified Datalog enhances traditional Datalog with negation, ensuring termination for polynomial time algorithms, offering a declarative approach for complex problem-solving.

Figure: Expressive power of logic programming increases from inner to outer circle¹

Relational algebra

Starting from the innermost circle, we have the foundation of relational data processing: relational algebra, which provides the fundamental operations for manipulating and querying structured data It serves as the theoretical basis for SQL queries. A limitation of SQL2 is the missing support of recursive queries. For example, conjunctive queries (finite union of select-project-join queries) cannot find all ancestor vertices of a given vertex³. Conjunctive queries are effective for retrieving data from relational databases by specifying conditions that must be simultaneously satisfied (hence “conjunctive”). But they are inherently non-recursive and cannot express recursive traversal operations needed for tasks such as graph traversal or hierarchical tree querying. Later on, SQL introduced support for recursive queries in the SQL:1999 standard, also known as SQL3. SQL3 added the WITH RECURSIVE clause, which allows defining recursive common table expressions (CTE) to perform recursive queries. This feature enables SQL to handle queries involving hierarchical or recursive data structures, such as traversing organizational charts, bill of materials, or network topologies. Thus, SQL3 started to support linear Datalog. Though it is possible to write recursive queries using SQL, it often feels somewhat “bolted on” and less elegant. For a more comprehensive discussion, check out my post on Recursive queries in SQL and Datalog.

Datalog

Moving outward, we encounter Datalog, a logic programming language that not only extends relational algebra but also inherently supports recursion. Datalog’s ability to define recursive rules empowers it to perform expressive queries and rule-based reasoning over relational data. While SQL3 supports recursive queries, Datalog was designed from the ground up with recursion as a core feature. Datalog’s syntax and semantics make it more natural and intuitive to express recursive queries and perform complex inferencing tasks. By enabling recursion, Datalog opens up avenues for tackling complex data relationships and hierarchical structures using expressive queries and rule-based reasoning over relational data.

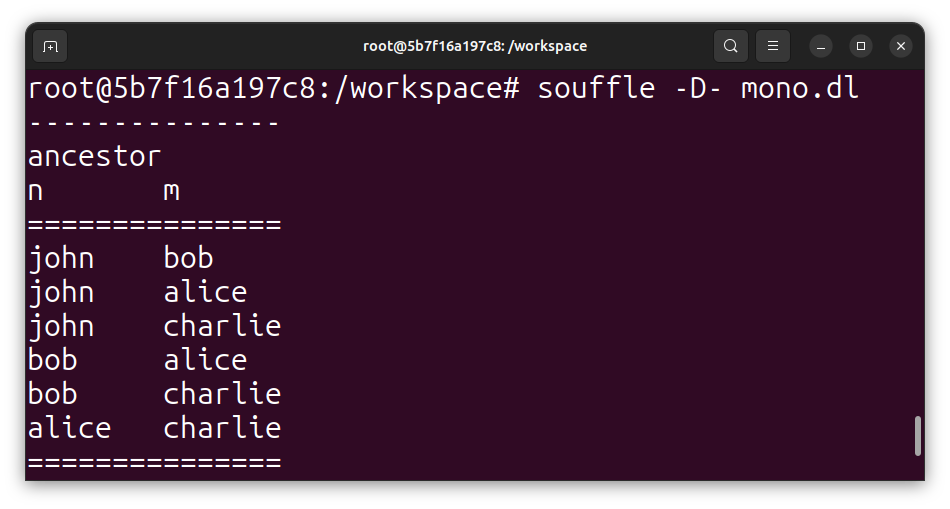
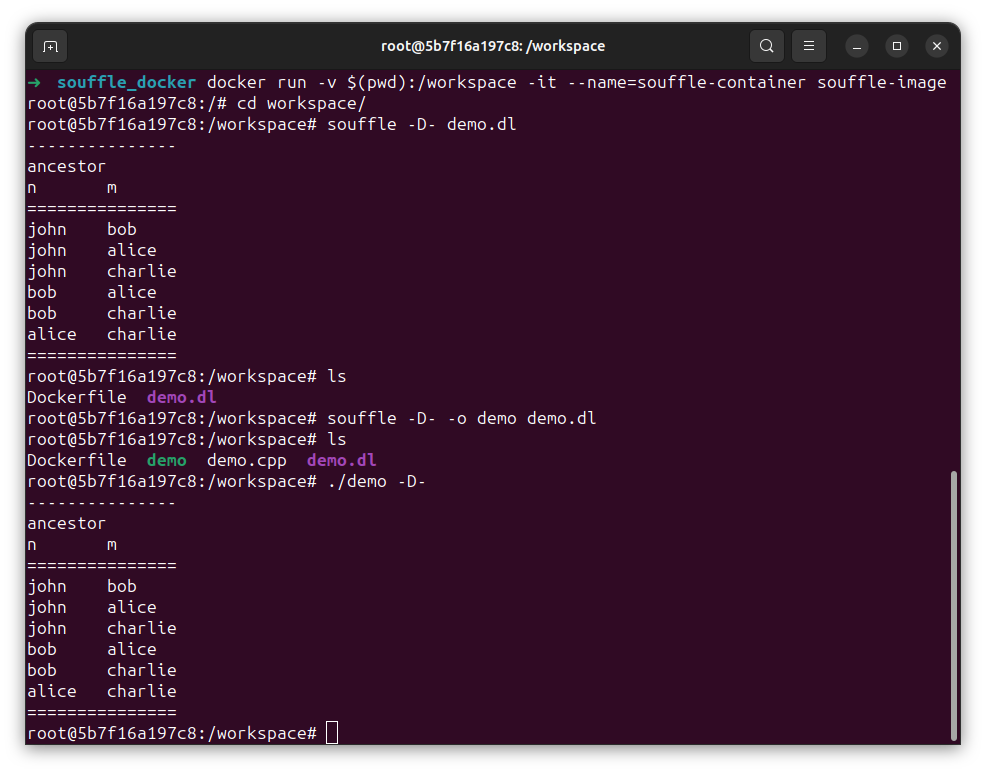
Here’s an example of a simple Datalog program that defines the ancestor relation recursively:

ancestor(X, Y) :- parent(X, Y).
ancestor(X, Z) :- parent(X, Y), ancestor(Y, Z).

In this program, the first rule (base rule) states that if X is a parent of Y, then X is an ancestor of Y. The second rule (recursive rule) says that if X is a parent of Y, and Y is an ancestor of Z, then X is also an ancestor of Z. This program can compute the transitive closure of the parent relation, enabling us to find all ancestors of a given person in a family tree.

Datalog engines utilizes semi-naïve evaluation techniques when handling recursive queries, optimizing the computation of recursive rules. This approach efficiently computes the least fixed-point of recursive rules by only processing newly derived facts in each iteration, avoiding redundant computations and enhancing performance. For these advantages, Datalog supports a wide range of applications for tackling complex data relationships and hierarchical structures which are beyond the capabilities of traditional SQL⁴.

Stratified Datalog

Expanding further, we encounter stratified Datalog, which enhances traditional Datalog with support for negation. By enforcing stratification, this variant ensures program termination, enabling the implementation of polynomial time algorithms. This makes it a powerful tool for solving complex problems in a declarative manner. Stratified Datalog supports negation, which allows for nonmonotonic reasoning and default assumptions. Nonmonotonic reasoning is a form of logical reasoning where adding new information to the knowledge base can invalidate or contradict previously derived conclusions. In other words, a statement that is true in a given knowledge base may become false or need to be revised when additional information is added to the knowledge base. This can be useful in certain types of inferencing tasks where we need to make assumptions based on incomplete information⁵. SQL3 and linear Datalog do not have built-in support for this type of nonmonotonic reasoning. To explore how monotonic and nonmonotonic reasoning in Datalog influences derived conclusions, check out my companion post: Monotonic and nonmonotonic reasoning in Datalog.

Prolog

At the outermost layer, we find Prolog, a logic programming language that extends beyond polynomial time algorithms, offering Turing completeness. Prolog allows for the specification of general-purpose algorithms and complex logical relationships. However, it sacrifices the guarantee of program termination, making it susceptible to non-termination in certain scenarios.

References