Characteristics
Non negative integers with a known maximum value
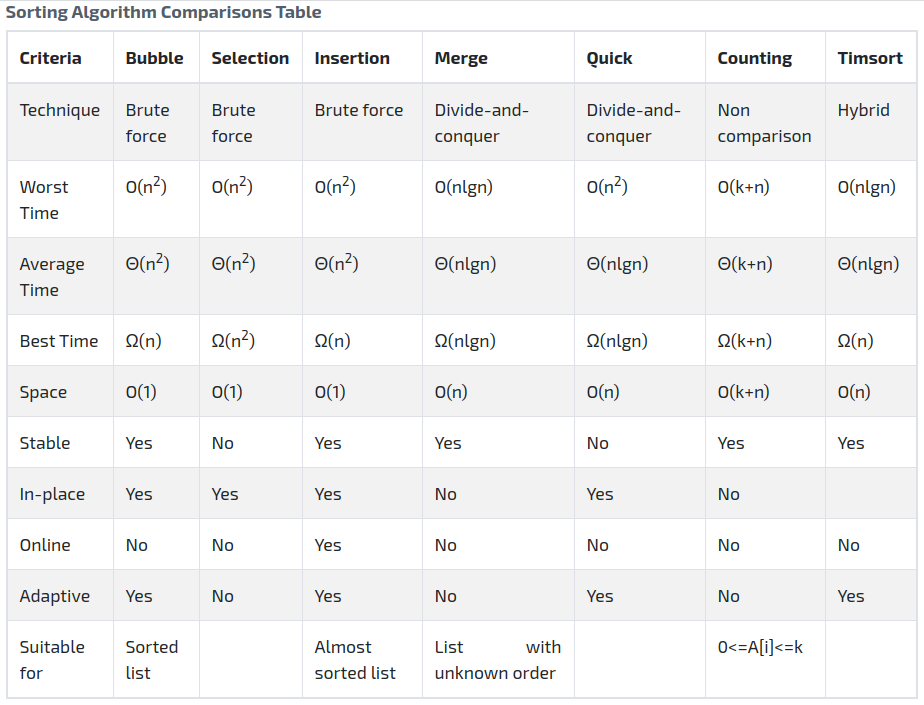
Counting sort can be applied if the input numbers are in the set {0, 1, .. ,k}, a set of non negative integers with a maximum value k.
No comparisons between elements
There are no comparisons between input elements that take place in counting sort. It uses array indexing to determine the relative order of the input numbers. It identifies the relative positions of each input element. For each element x, counting sort counts number of elements less than x. Then it uses this information to place element x directly into its correct position.
Linear time complexity
It has a linear time complexity.
- Worst Time complexity (Big-O):
O(k+n), wherek: maximum value of the integer set andn: total number of integers in the set. - Average Time complexity (Big-Theta):
Θ(k+n), wherek: maximum value of the integer set andn: total number of integers in the set. - Best Time complexity (Big-Omega):
Ω(k+n), wherek: maximum value of the integer set andn: total number of integers in the set. - Space complexity:
O(k+n), wherek: maximum value of the integer set andn: total number of integers in the set.
Stable
Counting sort is stable. Numbers with the same value appears in the output array as they appear in the input array. Let's take an input array A = [3, 0, 3] and k = 3. In the input array the value 3 occurs 2 times; at index 0 and 2. Counting sort ensures that in the output array the occurrences of 3 are placed as same order as of the input array.
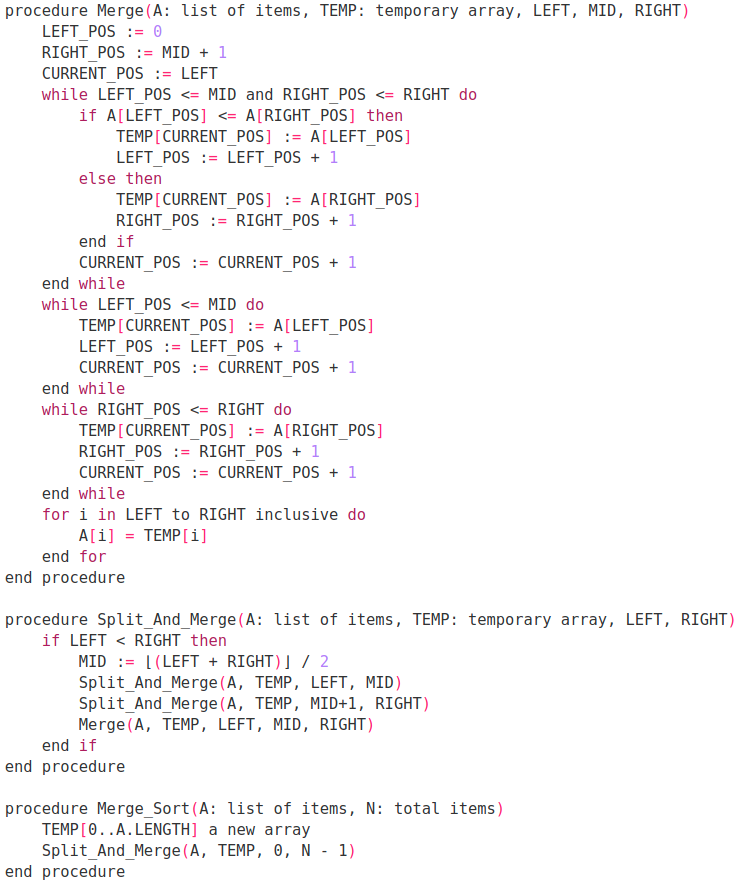
Algorithm Pseudocode
Counting_Sort(A, k)
let R[0 .. A.length-1] be a new array
for i=0 to A.length-1
R[i] = 0
let C[0 .. k] be a new array
for i=0 to k
C[i] = 0
for i=0 to A.length-1
C[A[i]] = C[A[i]]+1
for i=1 to k
C[i] = C[i-1] + C[i]
for i=A.length-1 to 0
R[C[A[i]]] = A[i]
C[A[i]] = C[A[i]] - 1
Implementation using Python 3
"""
Implementation of counting sort with test cases
"""
def get_sorted_list(numbers, max_value):
""" Returns sorted list of numbers using counting sort algorithm.
Arguments:
numbers -- list of integers, non negative and less than max_value
max_value -- integer
"""
sorted_numbers = [None] * len(numbers)
counts = [0] * (max_value+1)
for i in numbers:
counts[i] += 1
counts[0] -= 1
for i in range(1, max_value+1):
counts[i] += counts[i-1]
for i in numbers[::-1]:
sorted_numbers[counts[i]] = i
counts[i] -= 1
return sorted_numbers
if __name__ == "__main__":
A = [1, 5, 0, 0, 3, 3, 2, 1, 1]
k = 5
expected = [0, 0, 1, 1, 1, 2, 3, 3, 5]
assert expected == get_sorted_list(A, k), "Failed on A={}, k={}".format(A, k)
A = [9, 7]
k = 9
expected = [7, 9]
assert expected == get_sorted_list(A, k), "Failed on A={}, k={}".format(A, k)
Practice challenges
Easy difficulty challenges:
Medium difficulty challenges:
Reference
- Introduction to algorithms by Cormen, Thomas H and Leiserson, Charles E and Rivest, Ronald L and Stein, Clifford
- Timsort Wikipedia article
- Counting sort Wikipedia article
- timeit module documentation
Advertisement